Mecánica hamiltoniana — La mecánica hamiltoniana fue formulada en 1833 por William R. Hamilton. Como la mecánica lagrangiana, es una reformulación de la mecánica clásica. La mecánica hamiltoniana puede ser formulada por sí misma, usando los espacios simplécticos, sin… … Wikipedia Español
Ecuación de Hamilton-Jacobi — Saltar a navegación, búsqueda La ecuación de Hamilton Jacobi es una ecuación diferencial en derivadas parciales usada en mecánica clásica y mecánica relativista que permite encontrar las ecuaciones de evolución temporal o de movimiento . La… … Wikipedia Español
Hamiltoniano (mecánica clásica) — Para la versión cuántica del Hamiltoniano, véase Hamiltoniano (mecánica cuántica). El hamiltoniano es una función escalar a partir de la cual pueden obtenerse las ecuaciones de movimiento de un sistema mecánico clásico que se emplea en el enfoque … Wikipedia Español
Partícula en un potencial de simetría esférica — Saltar a navegación, búsqueda Una partícula en un potencial de simetría esférica, es un término para referirse a toda una serie de problemas o sistemas físicos interesantes en que una partícula está en un campo exterior central con simetría… … Wikipedia Español
Espacio fásico — de un sistema dinámico con estabilidad focal. En mecánica clásica, el espacio fásico, espacio de fases o diagrama de fases es una construcción matemática que permite representar el conjunto de posiciones y momentos conjugados de un sistema de… … Wikipedia Español
Integral de movimiento — Una integral del movimiento o constante del movimiento de un problema mecánico es una función de la posición y las velocidades (o equivalentemente de las coordenadas generalizadas y sus momentos conjugados) que es constante a lo largo de una… … Wikipedia Español
Transformación canónica — En mecánica hamiltoniana, una transformación canónica es un cambio de coordenadas canónicamente conjugadas que preserva la forma canónica de las ecuaciones de Hamilton, aun cuando la propia forma del Hamiltoniano no queda invariante. Las… … Wikipedia Español
Cantidad de movimiento — La cantidad de movimiento, momento lineal, ímpetu o moméntum es una magnitud vectorial, que en mecánica clásica se define como el producto de la masa del cuerpo y su velocidad en un instante determinado. En cuanto al nombre, Galileo Galilei en su … Wikipedia Español
Movimiento (física) — Para otros usos de este término, véase Movimiento. El movimiento es un cambio de posición respecto del tiempo. En mecánica, el movimiento es un fenómeno físico que se define como todo cambio de posición en el espacio que experimentan los cuerpos… … Wikipedia Español
Teorema de equipartición — Figura 1. Movimiento térmico de un péptido tipo hélice α. El movimiento vibratorio es aleatorio y complejo, y la energía de un átomo en particular puede fluctuar ampliamente. Sin embargo, el teorema de equipartición permite que se pueda calcular… … Wikipedia Español
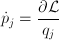 Si la coordenada generalizada es la posición lineal, el momento canónico conjugado correspondiente es el momento lineal o cantidad de movimiento 'mv'.
Si la coordenada generalizada es la posición angular, el momento canónico conjugado correspondiente es el momento angular.
Si la coordenada generalizada es la posición lineal, el momento canónico conjugado correspondiente es el momento lineal o cantidad de movimiento 'mv'.
Si la coordenada generalizada es la posición angular, el momento canónico conjugado correspondiente es el momento angular.